“无约束最优化问题，只需要最小化目标函数而无变量间的约束。”
一、数学表达
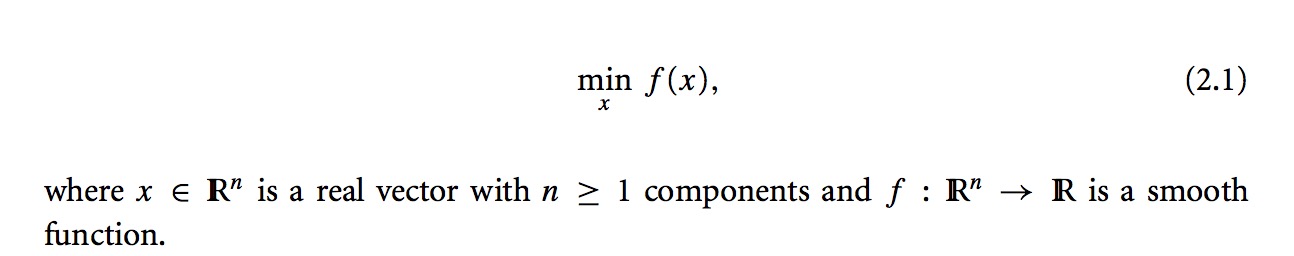举个例子:
假设有如下目标函数:
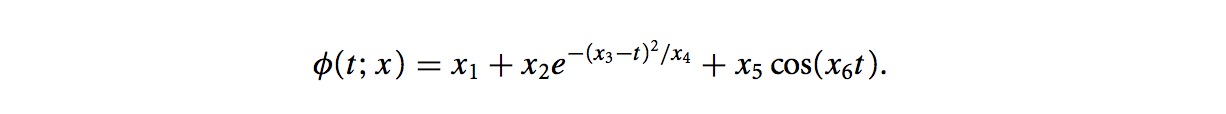φ(tj;x)如果要尽可能的接近观察值yj，定义它们之间的差:
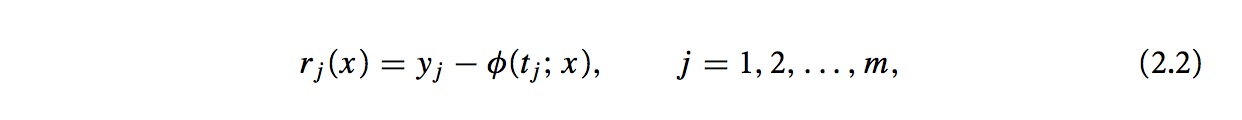其实我们要解决的是如下的问题:
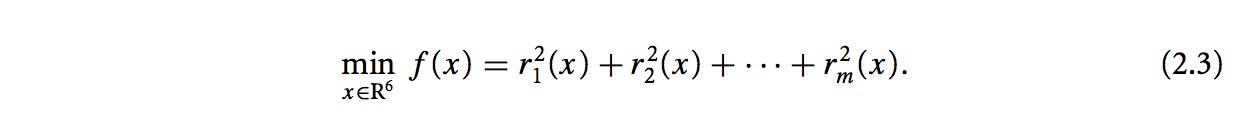局部最优解就是存在一个局部的x*使得它周围的x都有f(x*) < f(x).
二、局部最优解相关定理
1. 泰勒展开式:
一阶泰勒展开: f(x)≈f(x0)+∇f(x0)T(x−x0)
二阶泰勒展开: f(x)≈f(x0)+∇f(x0)T(x−x0)+12(x−x0)T∇2f(x0)(x−x0)
2. 局部最小值的一阶必要条件，如果x*为局部最优解并且函数f一阶可导，则在x*的邻域内∇f(x*)=0
3. 局部最优解的二阶必要条件，如果x*为局部最优解并且一阶和二阶可导，则∇f(x*)=0 并且∇2f(x)正定
证明: 定理2,3可以用反证法(略).
4. 局部最优的二阶充分条件：如果函数f在x*处满足∇f(x*)=0并且∇2f(x)正定，则x*为局部最优解.
5. 如果函数f为凸函数，则f的任何局部最优解都为全局最优解.
说明: 非平滑问题. 此问题不在讨论范围内，在此一般讨论二阶导数存在且连续的问题，对于非平滑甚至不连续的问题，一般会采用次梯度或者广义导数进行求解.
三、优化算法
A. 两种策略: 线搜索(Line Search)和信任域(Trust Region)
1. Line Search: 假设在某点xk，寻找方向pk和步长α使得f(xk+αpk)最小:<
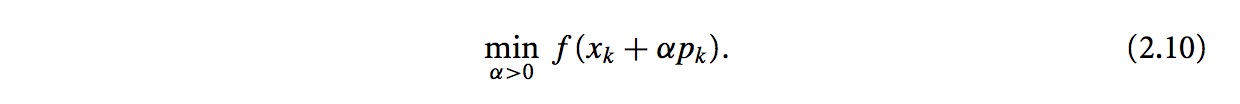2. Trust Region: 对于函数f在xk点的近似解mk，必须保证mk为一个较好的近似，所以必须在xk附近找到这样这样的mk(即最优解的近似解，必须在最优解附近才是好的近似解).所以要找到一个候选step p，可以通过近似解决下面的问题:
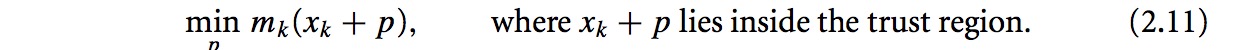信赖域如果过大，我们则缩小信赖域，信赖域定义满足||p||2≤Δ.2.11的式子写成二次方程的形式如下:
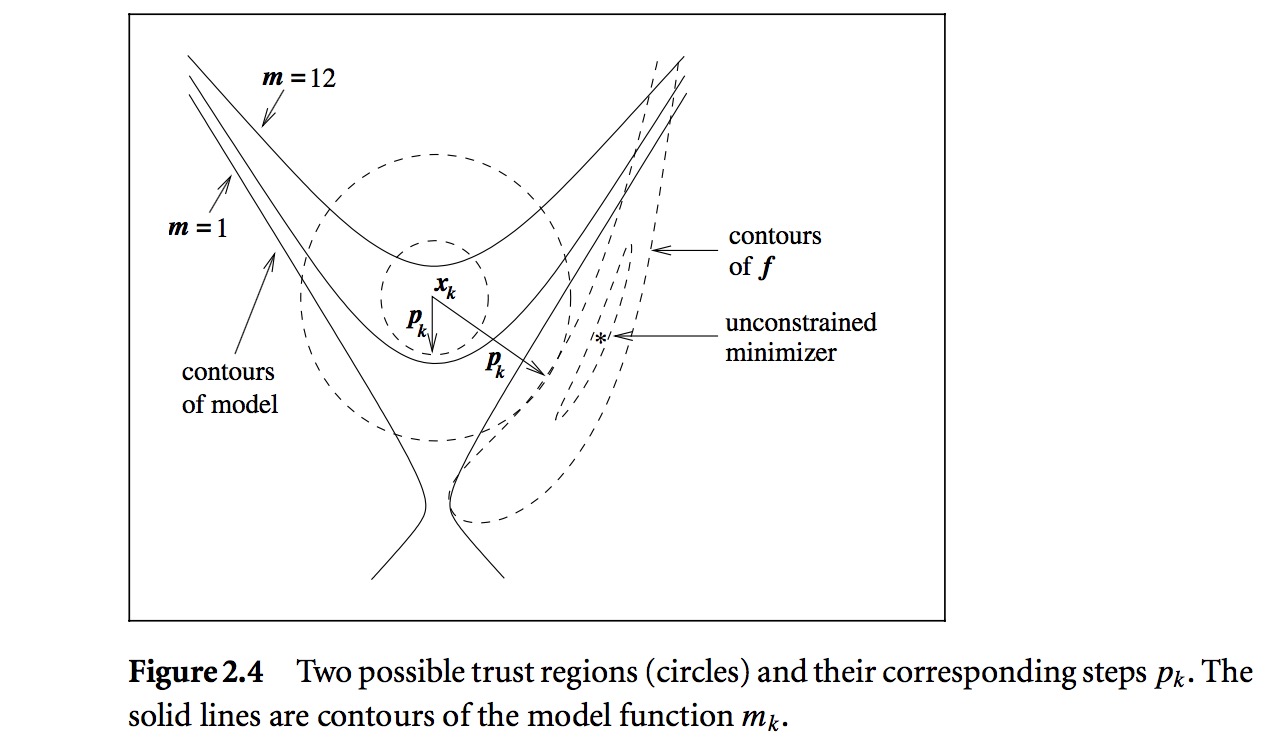
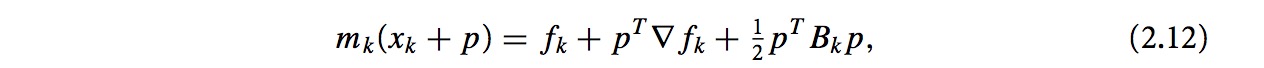下图是信赖域的示意图(线搜索和信赖域的区别主要是在选择方向和距离的顺序上，先搜索先选择方向，信赖域先选择距离):
B. Line Search中的搜索方向选择
1. 最速下降的方向，负梯度方向是最明显的选择，−∇fk。
search方向p，步长α，因此进行二阶泰勒展开
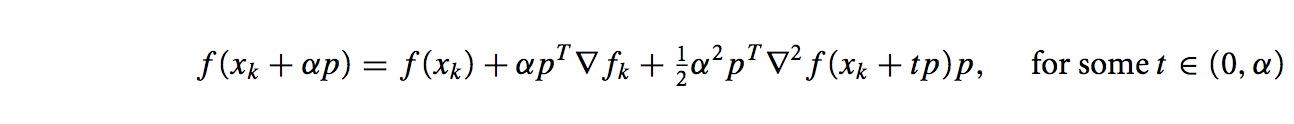由于∇2fk满足正定，因此等价于求解下面的问题
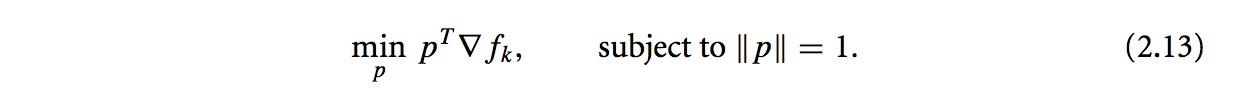至于为什么为负梯度方向，如下面推导
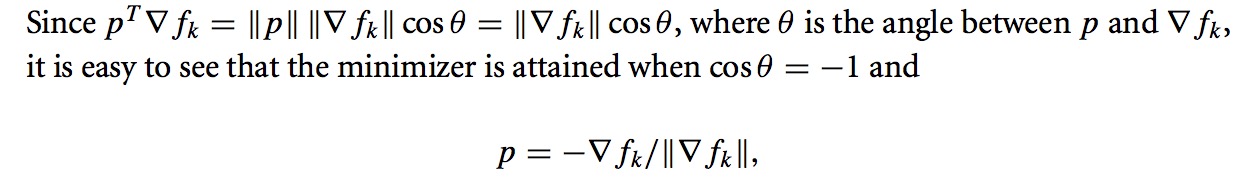2. 牛顿方向(Newton Direction)
最速下降方向来自于一阶泰勒展开项，而牛顿方向就是来自于二阶泰勒展开项
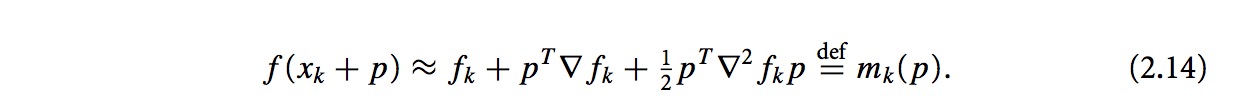
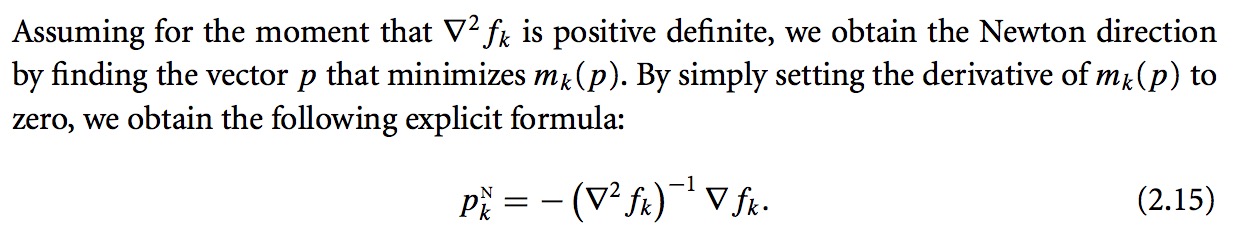上述的结论如何推导出来的?
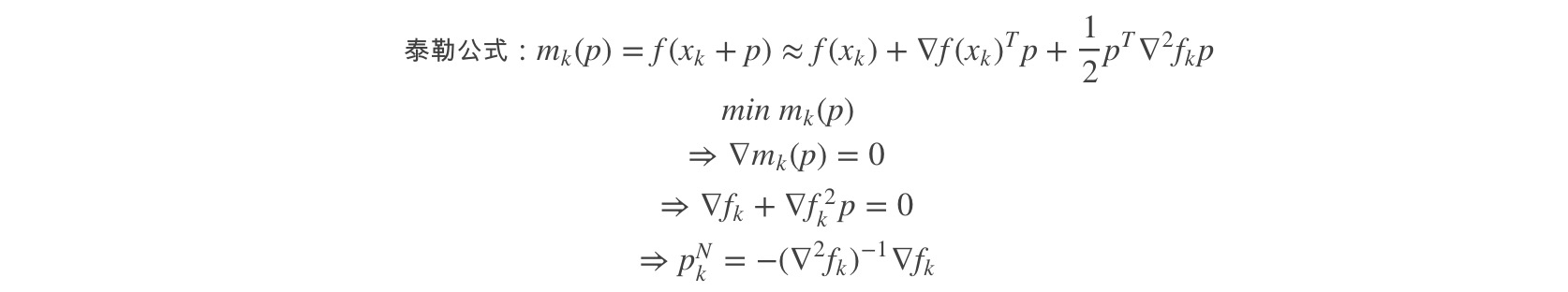由上式推导可得:
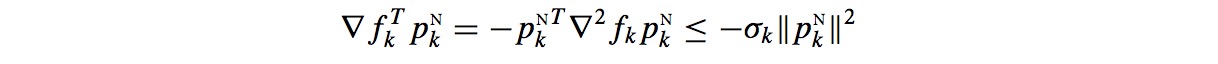只要∇fk不为0，牛顿方向则是下降方向。同理，如果为0，则牛顿方向就不存在(无法定义)，因此需要改变pk的定义(暂时不讨论)。牛顿方向依赖于计算Hessian 矩阵∇f2k，比较低效。
3. 拟牛顿方向(Quasi-Newton Direction)
拟牛顿方法提供了避免计算Hessian矩阵，并且收敛性也很好的方法。使用一个近似项Bk来代替Hessian 矩阵∇f2k的计算。改写∇f2kp的定义(泰勒展开):
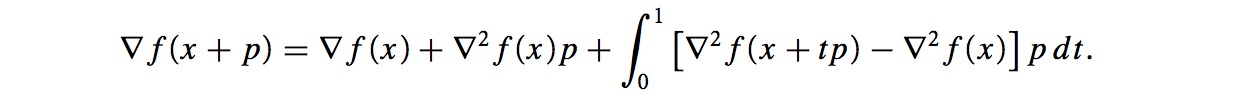∇f(.)是连续的，最后的一个整数项大小为o(||p||)。令x=xk && p=xk-1 - xk，则有
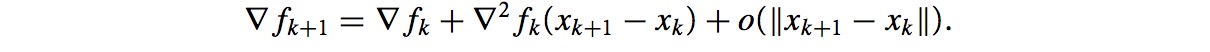xk和xk+1在解x*附近，并且∇2f是正定的，因此忽略最后的极小项，有
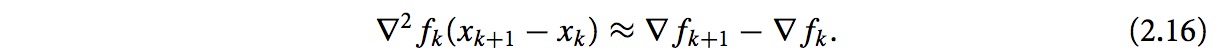用割线方程Bk+1sk = yk解释上式，其中sk+1 = xk+1 - xk, yk = ∇fk+1 - ∇fk.
这时我们只要逐步求解Bk+1，有两种方法:
a. symmetric-rank-one(SR1)
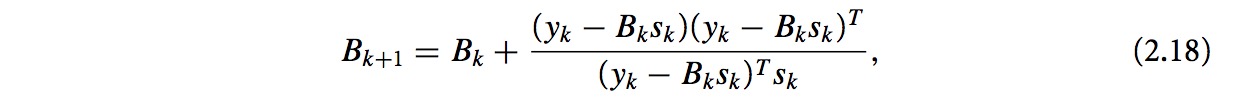b. BFGS
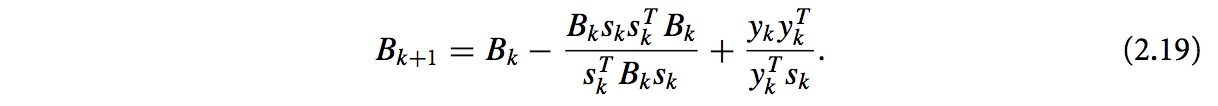根据割线方程，有:
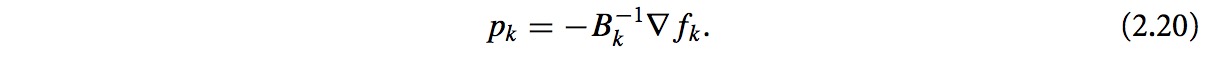令Hk=Bk-1，2.18和2.19变形得到下式:
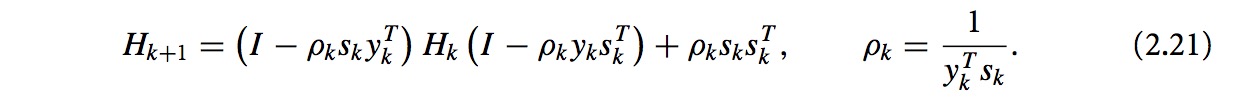求解pk，可以有pk=-Hk∇fk.
4. 非线性共轭梯度方向(nonlinear conjugate gradient methods)
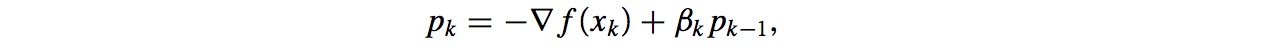共轭梯度方法是用来求解线性方程Ax=b的一种方法，等价于求解凸二次方程
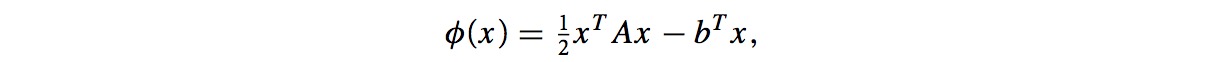因此该方法比最速下降法还要高效；最速下降法和非线性共轭梯度法虽然收敛效率没有牛顿和拟牛顿法那么高，但是它们不需要存储矩阵。
C. 信任域(Trust Region)模型
如果Bk = 0，则信赖域问题变成如下:
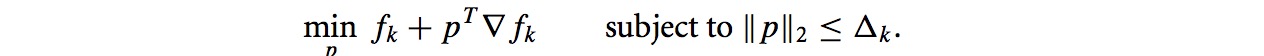求解pk，变成下式:
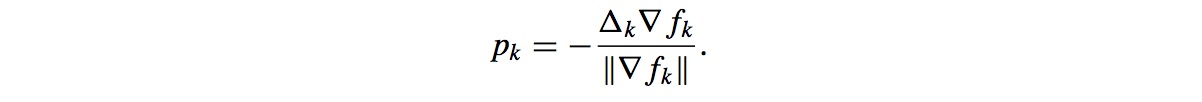
D. Scaling问题
1. 一个算法的表现好坏，其中一个很重要的问题就是scaling. 一个poorly scaled问题是指函数f(x)在某个方向上的变化比其他方向的变化，带来更大的函数值改动. (例子: f(x) = 109x1 + x2.)
2. 最速下降法就是poorly scaled算法, Newton法也会受到影响.因此scale invariance在算法中是很重要的，影响算法的收敛性。
