“数值优化为解最优化问题提供一种迭代算法思路,通过迭代逐渐接近最优解。”
一、简介
示例
1. 投资组合最优: 高回报,低风险
2. 自然界最优: 物理系统最低能量态
3. …
数值优化是通过迭代的方式解决最优化问题,是数学建模(modeling)的重要环节。
Modeling需要确定优化目标、目标依赖的变量以及变量间的约束关系。
二、数学描述
数学描述,优化问题是满足变量约束的前提下最小化or最大化一个目标函数。
Notation:
- x 是变量or参数(向量);
- f 是关于x的目标函数;
- ci 是x的限制条件。
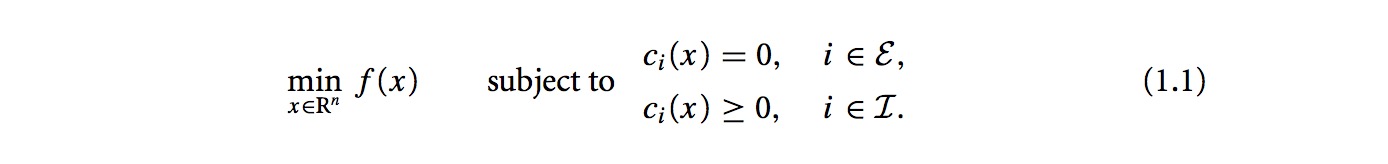
考虑一个简单问题:
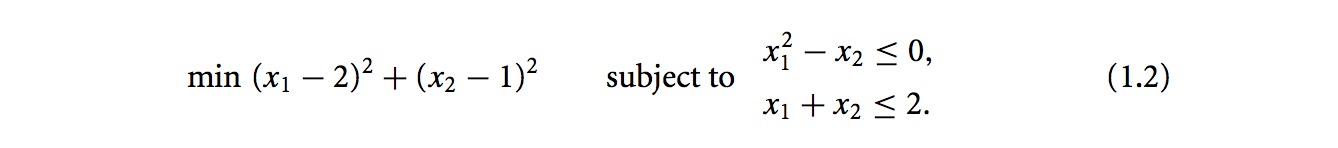
上面问题的几何表示:
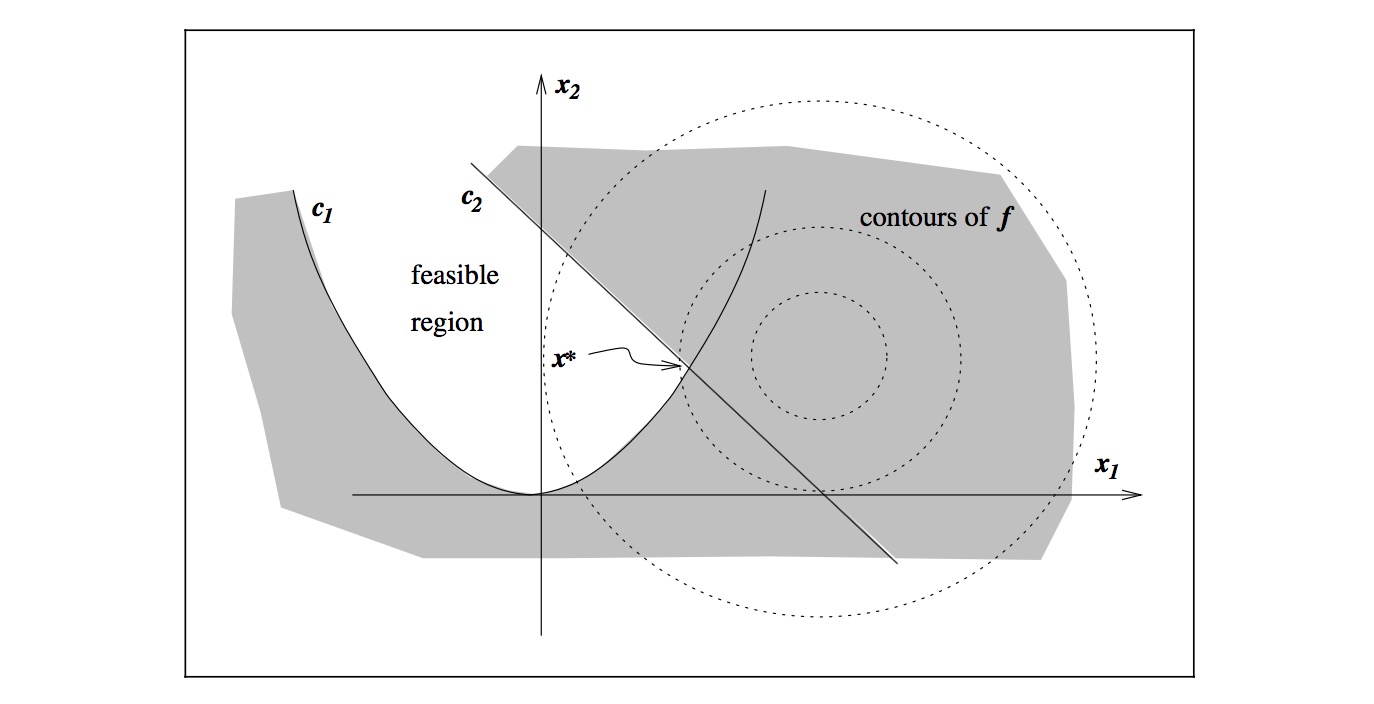
这个问题表示成1.1的形式:
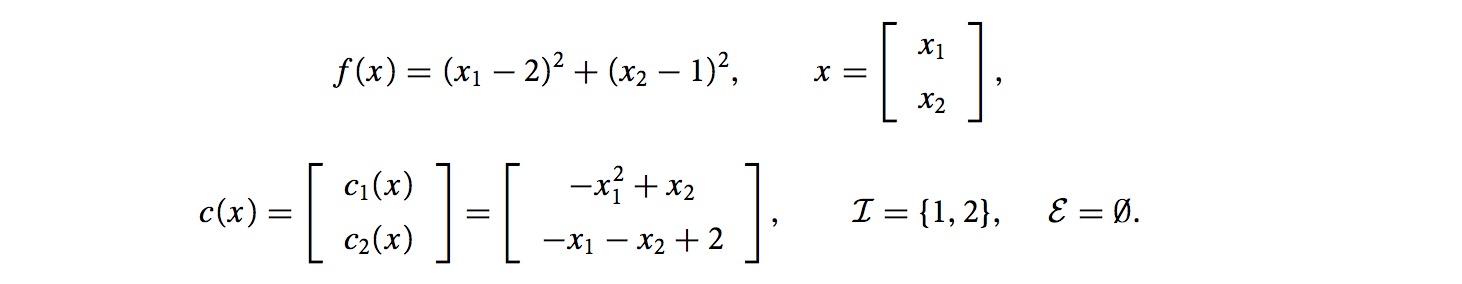
三、问题分类
根据目标函数或者约束条件的不同,最优化问题可以有如下分类:
* 连续/离散化优化问题
* 约束/非约束优化问题
* 线性/非线性优化问题
* 全局/局部优化问题
* 随机/确定性优化问题
四、凸优化
凸优化是优化问题中最基本的一种。实际中有很多问题都具有凸优化问题的特性,这种特性让问题更容易解。
凸优化的几个概念:
1. 凸集: 如果集合S为凸集,当且仅当 x∈S, y∈S 并且α(x)+(1−α)(y) inS;α∈[0,1]
2. 凸函数:如果函数f(x)为凸函数,当且仅当S为凸集,x∈S, y∈S; αf(x)+(1−α)f(y)≥f(αx+(1−α)y); α∈[0,1]
3. 严格凸函数,凸函数能够取到非等号,即α∈(0,1)
4. 凸优化问题:对于标准形式目标函数为凸函数,等式约束为线性约束;不等式约束为凹函数。
五、最优化算法
最优化算法是一个不断迭代的过程。起于一个初始参数(向量), 不断迭代改进预估值直至收敛,得到希望的解。
一般好的优化算法有如下几个特性:
1. 鲁棒性: 能在某类型的很多问题上都能有很好的解。
2. 高效性: 能在有限的计算时间和存储内完成求解。
3. 准确性: 能准确的求解问题,并且对数据中的错误不能过于敏感。
上述的几个特性之间本身可能存在一定的矛盾,例如要鲁棒性很可能会比较慢。